Going 3D

Edge Functions

In a previous section, I explored how to draw a line between 2 vertices using the Bresenham Algorithm. I also implemented a Scanline algorithm that fills a triangle’s pixels with some specific color. But this methods get very slow when dealing with hundreds of thousands of pixels which could be the case for a higher resolution triangle.

In this article, I want to implement a faster algorithm to do the same task. This is a very clever solution described by Juan Pineda - A Parallel Algorithm for Polygon Rasterization.

It uses something called edge functions to determine when a point/pixel is inside the area of a triangle.

Edge Functions

An edge function describes a line between 2 points in the screen. This line divides the screen in tree sections. The points that are to the left of the screen, the one to the right and the ones exactly on the line.

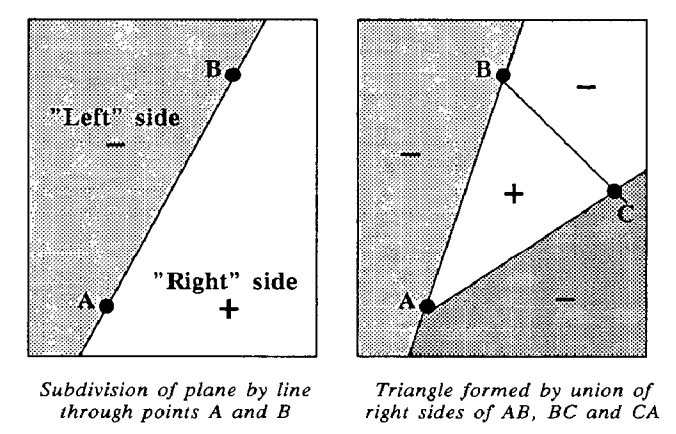
The edge function is described as follows:

E(x,y) = (x-X) dY- (y-Y) dX

This function has an interesting property, all points to the left produce a negative value, the points to the right produce a positive value and the points on the line produce a Zero value.

This is very useful because I can test a specific point against the three edge functions that represent a triangle and if all the results are positive or all the results are negative, I can be sure that the point is inside the triangle and I can draw the pixel.

This alone is already a big performance improvement because we do not have to build the triangle edges to rasterize it. We just need to find a clever way to go over all the points that are inside the triangle only once. One way is to simply create a rectangle using the max x and y and min x and y values of the triangle. This ensures that all the points inside that rectangle area cover the triangle.

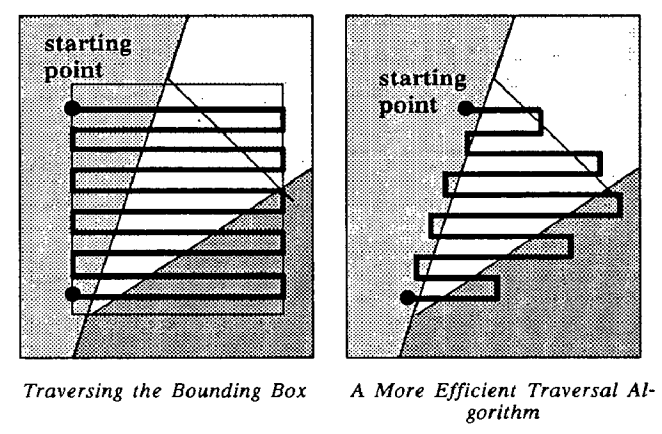
The image presented above shows two different ways to iterate over the triangle. I will use left one here but maybe I will expand this article with some other techniques later on.

First, I need to implement the edge function:

float TriangleEdgeFunction(Vec3 a, Vec3 b, Vec2 p) {
    return (b.x - a.x) * (p.y - a.y) - (b.y - a.y) * (p.x - a.x);
}

The next step is to go over each of the triangles that compose my object and rasterize it using the edge function to check if the points are inside the triangle. First, I will create a Triangle struct that holds all the information of the triangle.

struct Triangle {
    Vertex v1, v2, v3;
    Vec2 min, max;
};

I will need the min and max values to scan the triangle as mentioned before.

After performing the transformations of each of the triangle’s vertices, I can create a triangle and add it to the triangles of this object.

std::vector<Triangle> triangles;

...

Vec2 vMin = {
    (float)std::max(
        0, static_cast<int>(std::floor(std::min({v1.x, v2.x, v3.x})))),
    (float)std::max(
        0, static_cast<int>(std::floor(std::min({v1.y, v2.y, v3.y})))),
};
Vec2 vMax = {
    (float)std::min(r->width - 1, static_cast<int>(std::ceil(
                                      std::max({v1.x, v2.x, v3.x})))),
    (float)std::min(r->height - 1, static_cast<int>(std::ceil(
                                       std::max({v1.y, v2.y, v3.y})))),
};

Triangle triangle = {
    .v1 = Vertex{Vec3{v1.x, v1.y, v1.z}, v1Norm, v1Color},
    .v2 = Vertex{Vec3{v2.x, v2.y, v2.z}, v2Norm, v2Color},
    .v3 = Vertex{Vec3{v3.x, v3.y, v3.z}, v3Norm, v3Color},
    .min = vMin,
    .max = vMax,
    .area =
        TriangleEdgeFunction(Vec3{v1.x, v1.y, v1.z},
                             Vec3{v2.x, v2.y, v2.z}, Vec2{v3.x, v3.y}),
};

triangles.push_back(triangle);

Now, I just need to create a function called Renderer_RasterizeTriangles that runs the rasterization procedure.

void Renderer_RasterizeTriangles(Renderer *r,
                                 const std::vector<Triangle> &triangles) {
    for (const auto &triangle : triangles) {
        // Determine winding
        bool clockwise = triangle.area < 0;

        // Rasterize only within tile bounds
        for (int y = triangle.min.y; y <= triangle.max.y; y++) {
            for (int x = triangle.min.x; x <= triangle.max.x; x++) {
                Vec2 p = {x + 0.5f, y + 0.5f};

                float w0 = TriangleEdgeFunction(triangle.v1.coords,
                                                triangle.v2.coords, p);
                float w1 = TriangleEdgeFunction(triangle.v2.coords,
                                                triangle.v0.coords, p);
                float w2 = TriangleEdgeFunction(triangle.v0.coords,
                                                triangle.v1.coords, p);

                // Check inside based on winding
                bool inside = clockwise ? (w0 <= 0 && w1 <= 0 && w2 <= 0)
                                        : (w0 >= 0 && w1 >= 0 && w2 >= 0);

                if (inside) {
                    // Render the pixel
                }
            }
        }
    }
}

Notice that I use the area of the triangle to check which is the winding of the triangle. This is done to cover the cases when all points give a negative value on the edge function or all give a positive value.