Graphics Rasterizer

Drawing Lines

Now that I have a renderer I want to start drawing things on the screen.

The most basic thing I can think of rendering is 1 pixel, but this wouldn’t be to interesting. So the next thing to render would be a line between 2 points in the screen.

First I need to select 2 points on the screen. For this I have created a struct that stores 2D coordinates a Vec2:

struct Vec2 {
    float x;
    float y;
};

I will also add a function to the renderer that draws a line between 2 points:

void Renderer_DrawLine(
    Renderer *r,
    Vec2 p1,
    Vec2 p2,
    uint32_t color,
);

The function also accepts a color parameter that will be used to paint all the points on the line.

For the implementation I will explore a very famous algorithm.

Bresenham’s Line Algorithm

The Bresenham’s line algorithm algorithm determines the points in between 2 points that approximate to a straight line. It is very efficient as it uses only integer addition, subtraction, and bit shifting.

This algorithm uses an incremental error approach. It chooses an axis to iterate from and then it picks a possible increment on the opposite axis and checks if it meets the error threshold.

This is an example and pseudo-code. Imagine drawing a line from (0,1) to (6,4).

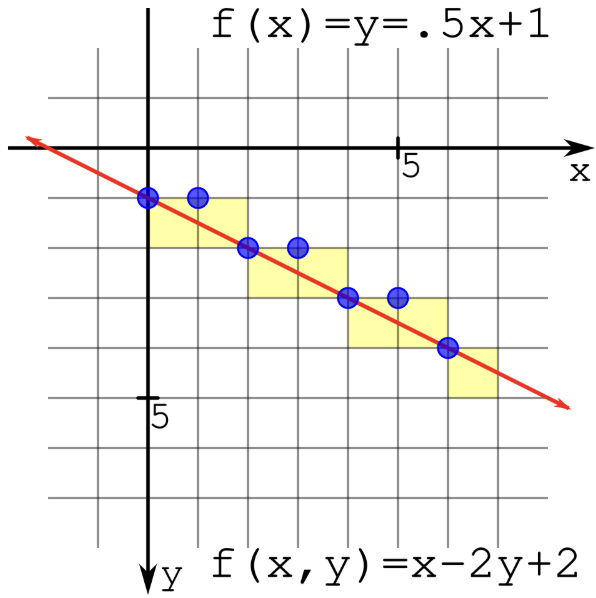
I start iterating from X0 to X1, so from 0 to 6 in this case and the y value starts at Y0 so at 1. At every step I need to check the error value to see if it is greater than 0. When the error value is greater than 0 the y value is incremented by 1.

plotLine(x0, y0, x1, y1)
    dx = x1 - x0
    dy = y1 - y0
    D = 2*dy - dx
    y = y0

    for x from x0 to x1
        plot(x, y)
        if D > 0
            y = y + 1
            D = D + (2 * (dy - dx))
        else
            D = D + 2*dy
        end if

I leave the derivation of the error value D formula out of the scope from this guide. I used the wikipedia’s article to underhand how it works and derive my implementation.

Now, I can finally draw a line:

void Renderer_DrawLine(
    Renderer *r, Vec2 p1, Vec2 p2, uint32_t color) {
    if (r == nullptr) {
        return;
    }

    int dx = p2.x - p1.x;
    int dy = p2.y - p1.y;

    int yi = 1;
    if (dy < 0) {
        yi = -1;
        dy = -dy;
    }

    int d = (2 * dy) - dx;
    int y = p1.y;

    for (int x = p1.x; x <= p2.x; ++x) {
        Renderer_SetPixel(r, x, y, 1.0f, color);

        if (d > 0) {
            y += yi;
            d = d + (2 * (dy - dx));
        } else {
            d = d + 2 * dy;
        }
    }
}

Next, I just need to call this function with two points in the screen.

Vec2 p1 = {80.0f, 80.0f};
Vec2 p2 = {130.0f, 50.0f};
uint32_t color = 0xFF0000;

Renderer_DrawLine(&renderer, p1, p2, color);

When running the program I see my first line:

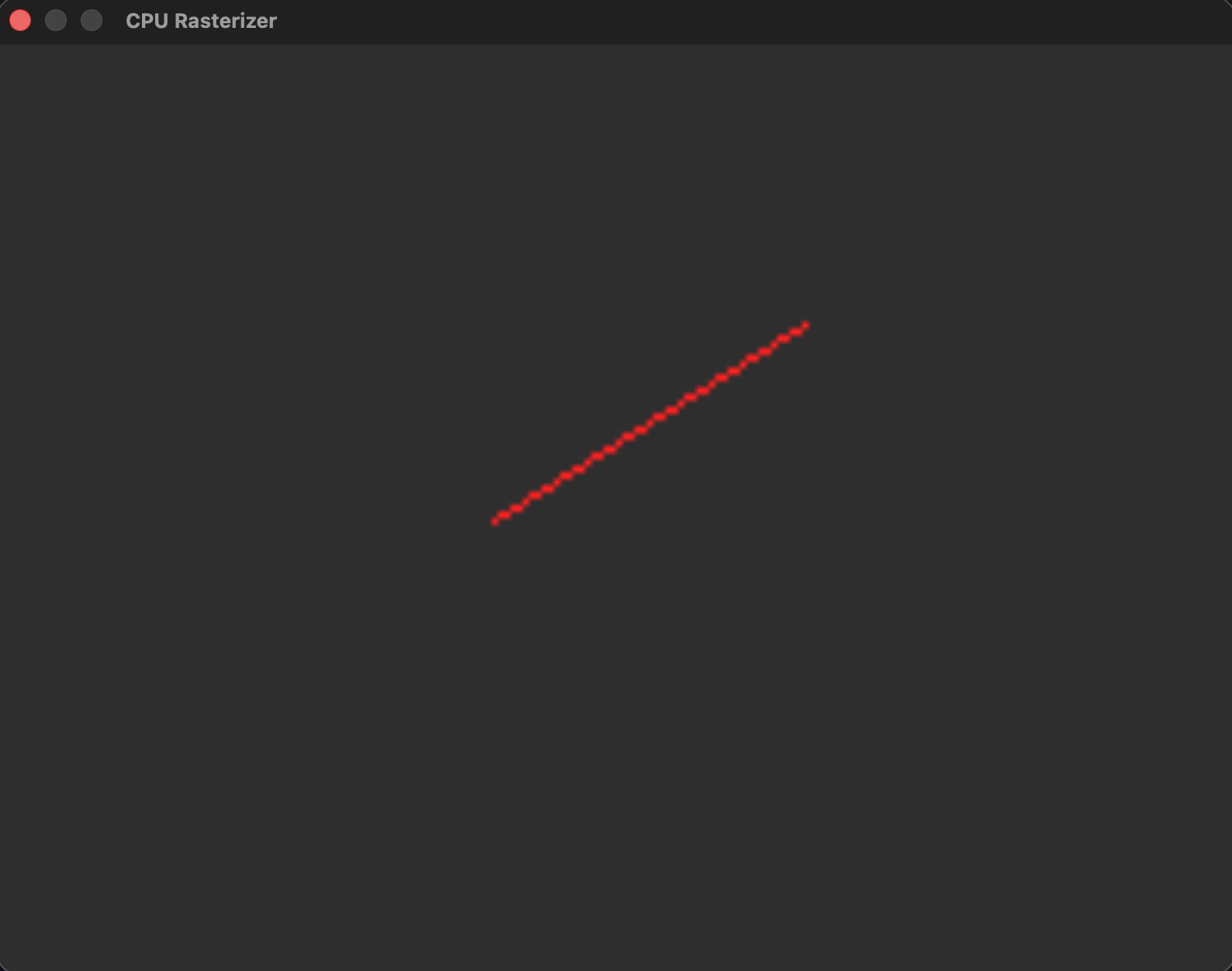
The previous function is only valid for the case where lines start at the origin with a slope between 0 and 1. To draw lines going in different directions and different slopes we need to draw them a bit different.

void Renderer_DrawLine(
    Renderer *r, Vec2 p1, Vec2 p2, uint32_t color) {
    if (r == nullptr) {
        return;
    }

    if (abs(p2.y - p1.y) < abs(p2.x - p1.x)) {
        if (p1.x > p2.x) {
            Renderer_DrawLineHorizontal(r, p2, p1, color);
        } else {
            Renderer_DrawLineHorizontal(r, p1, p2, color);
        }
    } else {
        if (p1.y > p2.y) {
            Renderer_DrawLineVertical(r, p2, p1, color);
        } else {
            Renderer_DrawLineVertical(r, p1, p2, color);
        }
    }
}

void Renderer_DrawLineHorizontal(
    Renderer *r, Pixel p1, Pixel p2, uint32_t color) {
    if (r == nullptr) {
        return;
    }

    int dx = p2.x - p1.x;
    int dy = p2.y - p1.y;

    int yi = 1;
    if (dy < 0) {
        yi = -1;
        dy = -dy;
    }

    int d = (2 * dy) - dx;
    int y = p1.y;

    for (int x = p1.x; x <= p2.x; ++x) {
        Renderer_SetPixel(r, x, y, 1.0f, color);

        if (d > 0) {
            y += yi;
            d = d + (2 * (dy - dx));
        } else {
            d = d + 2 * dy;
        }
    }
}

void Renderer_DrawLineVertical(
    Renderer *r, Vec2 p1, Vec2 p2, uint32_t color) {
    if (r == nullptr) {
        return;
    }

    int dx = p2.x - p1.x;
    int dy = p2.y - p1.y;

    int xi = 1;
    if (dx < 0) {
        xi = -1;
        dx = -dx;
    }

    int d = (2 * dx) - dy;
    int x = p1.x;

    for (int y = p1.y; y <= p2.y; ++y) {
        Renderer_SetPixel(r, x, y, 1.0f, color);

        if (d > 0) {
            x += xi;
            d = d + (2 * (dx - dy));
        } else {
            d = d + 2 * dx;
        }
    }
}

I can easily draw a triangle now by drawing 3 lines between 3 points.

Vec2 p1 = {80.0f, 80.0f};
Vec2 p2 = {130.0f, 50.0f};
Vec2 p3 = {140.0f, 90.0f};
uint32_t color = 0xFF0000;

Renderer_DrawLine(&renderer, p1, p2, color);
Renderer_DrawLine(&renderer, p2, p3, color);
Renderer_DrawLine(&renderer, p3, p1, color);

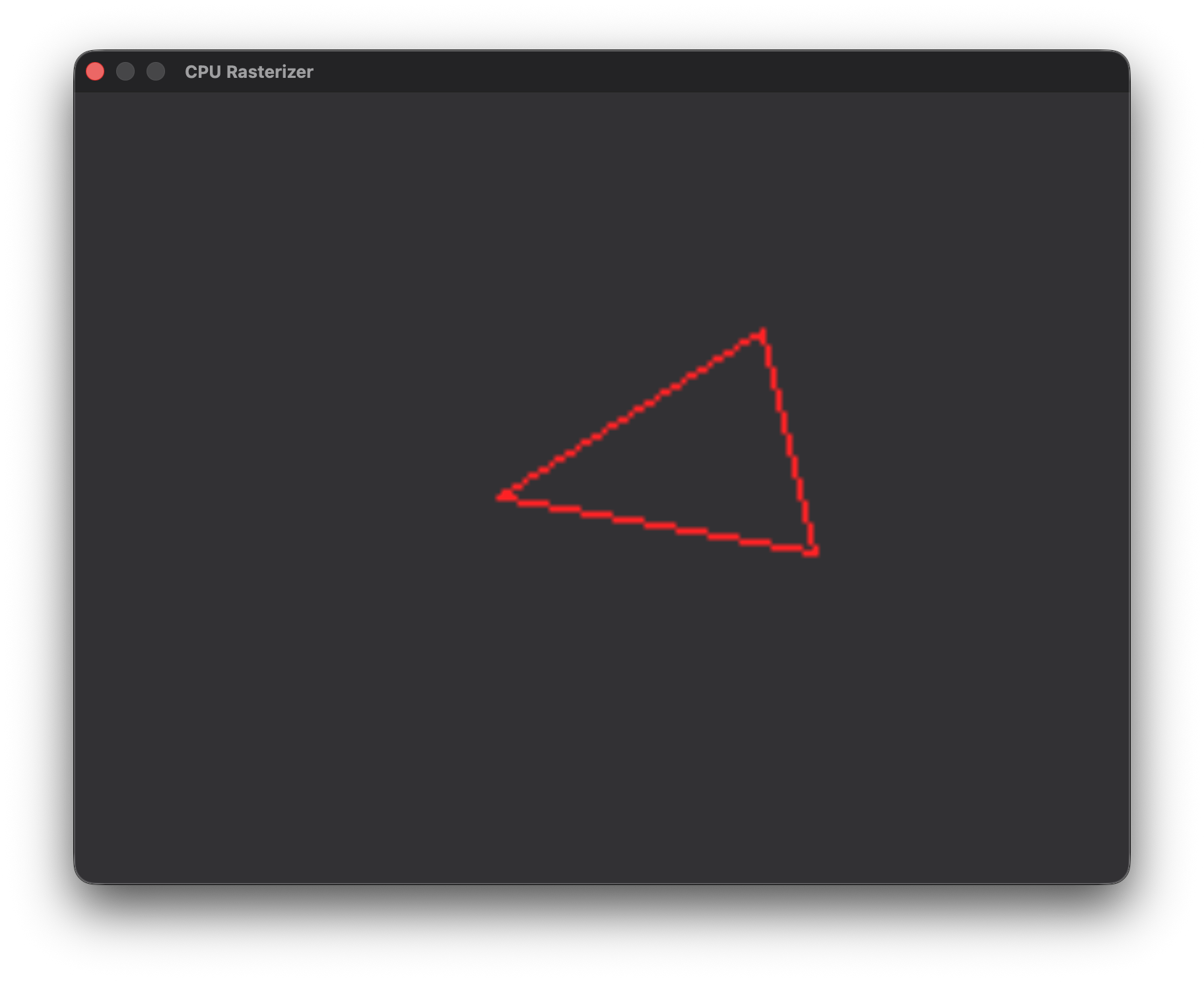
Now, I can go on to fill the triangle in the next article.